Expansion of a Product of Binomials

There are basically two methods to approach the expansion or removal of brackets in a product of the form

(ax + b)(cx + d). (By the way, you should know them by now)

Method 1: FOIL Method

First – the product of the two first terms in each binomial

Outer – the product of the two outer terms when viewed as shown above

Inner – the product of the two inner terms when viewed as shown above

Last – the product of the two last terms in each binomial.

Method 2: Turn the original problem of multiplying two binomials into a problem of expanding two products of a monomial and a binomial (ie. (ax + b)(cx + d) = ax (cx + d) + b(cx + d)).

Example 1:

Expand (3x – 2y) (4x + 7y) .

solution:

(3x – 2y) (4x + 7y) = First + Outer + Inner + Last

= (3x)(4x) + (3x)(7y) + (-2y)(4x) + (-2y)(7y)

= 12x ² + 21xy – 8xy – 14y ²

= 12x ² + 13xy – 14y ²

Remark 1:

There are some special cases of binomial products which you can now understand. Here we’ll just list them. In what follows, the symbols a, b, c, and d stand for specific numbers.

The product of two binomials involving just a single variable x can always be simplified to a second degree polynomial (or a trinomial, if you like). In general

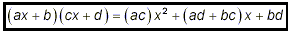
Our first example demonstrated this.

If the coefficients of x in the binomials are both equal to 1, then a somewhat simpler result occurs:

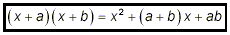
Notice the pattern here:

Example 2:

(x + 5)(x + 7) = (1)x 2 + (5 + 7)x + (5)(7) = x 2 + 12x + 35.

Example 3:

(x + 5)(x – 7) = (1)x 2 +[5 + (-7) ]x + (5)(-7) = x 2 – 2x – 35.

You will get the same result in these cases using either of our earlier method 1 or method 2. Squaring a binomial is, of course, a special case of multiplication involving the same factor twice. The simplest instance of squaring a binomial is

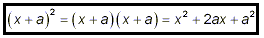
Notice the pattern here:

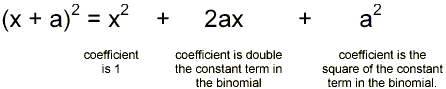
Example 4:

(x - 7) ² = (1)x ² + (2)(-7)x + (-7) ² = x ² - 14x + 49 .

When the coefficients of x in the two binomials are equal, and the constant terms in the two binomials are numerically identical, but of opposite sign, the simplified expansion of the product is itself a binomial:

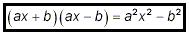
Example 5:

(2x + 3)(2x – 3) = (2x)(2x) + (2x)(-3) + (3)(2x) + (3)(-3)

= 4x ² – 6x + 6x – 9

= 4x ² – 9

or, using the pattern shown in the boxed formula just above,

(2x + 3)(2x – 3) = (2) ² x ² – (3) ² = 4x ² – 9 .

You can see what happens in this case: the “inner” and “outer” contributions (when using the FOIL method) are identical, but of opposite sign, so they cancel out, leaving just the other two terms.

We will exploit these special patterns to some extent later when we consider the operation of factoring.

Remark 2:

Method 2 described above is more general and more powerful than the FOIL method because it is easily extendable to products involving factors with more than two terms. Such problems are a bit beyond the scope of this lesson, but it is worth presenting one example here to help you understand the principle.

Example 6:

Expand (3x + 5y)(2x + 8y – 7z) .

solution:

(3x + 5y)(2x + 8y – 7z)

= (3x + 5y)(2x) + (3x + 5y)(8y) + (3x + 5y)(-7z)

= (2x)(3x + 5y) + (8y)(3x + 5y) + (-7z)(3x + 5y)

= (2x)(3x) + (2x)(5y) + (8y)(3x) + (8y)(5y) + (-7z)(3x) + (-7z)(5y)

= 6x ² + 10xy + 24xy + 40y ² – 21xz – 35yz

= 6x ² + 34xy + 40y ² – 21xz – 35yz.

It would be difficult to come up with a generalization of the FOIL method to handle this example (we’d need six meaningful words that are easy to remember, but distinguish between middles, and firsts, and lasts, and inners and outers, and so forth). However, the application of Method 2 occurs quite naturally here, and you can probably even see how we would handle products involving factors with even more terms.