Values of Symbols for Which Fractions are Undefined
Here we simply remind you that several properties of fractions
of the following special forms continue to apply to fractions in
which the numerator and/or denominator are algebraic expressions.
We have already discussed and illustrated these properties with
reference to numerical fractions. They are
| |
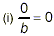 |
as long as b is not also equal to zero. |
| |
|
|
| |
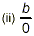 |
is undefined (or infinite) as long as b
is not also equal to zero. |
| and |
|
|
| |
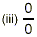 |
is undefined (or indeterminate) |
The words “undefined” or “indeterminate”
here do not mean that people are presently not clever enough to
figure out what these expressions must mean. Instead, they
indicate that such expressions are numerical nonsense – it
is impossible to interpret them in a way that makes numerical
sense, or that assigns to them an actual meaningful numerical
value.
From this list, we see that essentially, whenever the
denominator of a fraction evaluates to zero, we may speak of the
value of that fraction as being undefined.
The slight twist with algebraic fractions is that if the
denominator is an algebraic expression, then the value of the
denominator depends on the values assigned to any symbols that
are present. For some values of those symbols, the denominator
may evaluate to a nonzero value and so no problem arises.
However, there may be some values of the symbols for which the
denominator does evaluate to zero, and so the fraction as a whole
becomes undefined.
Example 1:
For what values of x is the fraction 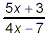 undefined? undefined?
solution:
Fractions are undefined when the denominator has a value of
zero. Thus, this fraction will be undefined for any value of x
that makes
4x – 7 = 0
But this is just a very simple equation. Solving, we get
4x = 7
and so
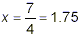
Checking
4(1.75) – 7 = 7 – 7 = 0.
Thus, the given fraction is undefined only when x = 7 / 4 =
1.75
Example 2:
For what values of x is the fraction 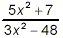 undefined? undefined?
solution:
Again, we need only look at the denominator. The fraction as a
whole will be undefined whenever the denominator is equal to
zero, that is, whenever
3x 2 – 48 = 0
This is an equation for x which is not too hard to solve:
3x 2 – 48 = 0
gives
3x 2 = 48
and so
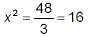
So any value of x that can be squared to give 16 will satisfy
this equation. But 16 = 4 2 and 16 = (-4) 2
, so there would appear to be two values of x that satisfy this
equation and hence make the denominator of the original equation
equal to zero:
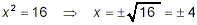
So, the original fraction is undefined if x = +4 and if x =
-4. (You can check by direct substitution that both of these
values of x result in the original fraction having the form b / 0,
where b 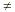 0.) 0.)
A final reminder: fractions are undefined in the way
we’ve been discussing here only when the denominator
evaluates to zero. If the numerator evaluates to zero, but the
denominator is nonzero, the fraction itself just has the value of
zero and no problem results. Thus, in Example 1 above, if we
substitute x = -3 / 5, we get:
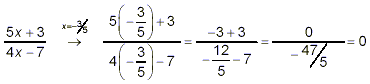
This poses no mathematical problem. “Undefinedness”
of the sorts referenced in items (ii) and (iii) of the list at
the beginning of this note only arises when the denominator
evaluates to zero.
|